상관을 구하려고 하는 두 변수 중에서 하나의 변수나 혹은 두 변수 모두가 서열척도일 경우에는 Spearman 등위상관계수(Spearman rank correlation coefficient)를 산출하는 것이 적합하다. 또한 점수분포가 극히 이질적이고 등위 이외에는 별다른 의미를 갖지 못할 때도 Spearman 상관계수를 산출한다. 그리고 산술평균보다는 중앙값을 구하는 것이 더 적절한 자료인 경우에 산출하는 상관계수가 Spearman 상관계수이다.
두 변수가 1부터 N까지 등위를 가질 때 Spearman 상관계수 rs를 구하는 공식은 다음과 같다.
![]()
여기에서 di는 두 변수의 i번째 점수에 해당되는 두 등위 사이의 차를 나타내며, N은 사례수이다. 두 변수가 등위 1부터 N까지 점수가 주어졌을 때, Spearman rs는 Pearson r과 대수적으로 동일하다. 즉 등위로 주어진 자료를 가지고 산출한 r과 rs의 값은 동일하다.
표 6. 5. 1은 Pearson r을 산출한 바 있는 그림 6. 1. 3의 자료(r=.884)를 사용하여 Spearman rs를 산출하는 절차를 제시하고 있다. 먼저 X와 Y점수를 각각 등위로 바꾼다. 이 때 등위가 같은 점수에 대해서는 평균 등위를 부여한다. 그리고 짝진 점수의 등위차(di)의 제곱합(Σdi²)을 구한 다음, 이를 Spearman rs 공식에 대입한다.
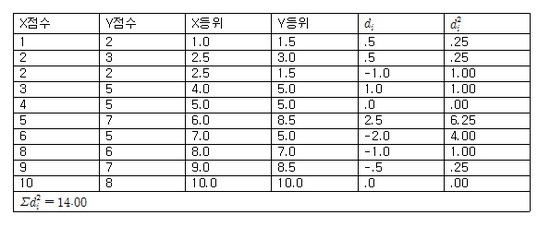
[표 6. 5. 1: Spearman 등위상관계수의 계산]
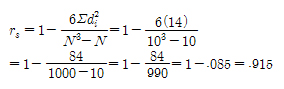
같은 자료를 가지고 산출한 r과 rs의 값이 약간의 차이가 있는 것은, 자료샹에 동일한 등위가 있었기 때문이다. 일반적으로 등간자료를 가지고는 Pearson r을 계산하는 것이 상례이다. 그러나 Spearman rs는 계산이 간편하고, Pearson r의 근사치가 된다. 또한 Spearman rs는, 점수는 연속적인 분포를 가져야 하며, 한 변수의 점수 내에서는 동일한 등위를 갖지 않는다는 가정을 만족하여야 하는 비모수적 통계방법이다. 따라서 동일한 등위가 많이 나타난 자료를 가지고 계산된 Spearman rs는 문제가 된다. 그러나 동일한 등위가 그리 많지 않을 때는 크게 영향을 받지 않는다.
*출처: 사회과학 연구를 위한 통계방법
1) 상관 계수 : 관계의 분석에서 가장 중심이 되는 개념은 두개 이상의 변수들끼리 어떠한 관계에 의해 공변(covariate)하는 현상에 대해 연구하는 것이다. 상관 관계는 '관계가 있다' 혹은 '관계가 없다' 라는 흑과 백의 결정으로 끝나는 것이 아니라 어느 정도 관계가 있느냐에 관심을 둔다. 그러한 관계를 나타내는 지수를 상관 계수(correlation coefficient)라고 부르며, 이것의 기호난 'r'이다.
상관계수(correlation of coefficient) : 공분산의 크기는 X와 Y의 단위에 따라 달라지므로 단위에 관계 없이 X와 Y의 관계를 측정하기 위하여 공분산을 X와 Y의 표준 편차로 나누어 준 값이다. 그리고 상관 관계 계수값은 -1에서 +1의 범위를 갖는다 |r| < 0.2 이면 관계가 없거나 무시해도 좋은 수준이며, 0.4 정도이면 약한관계, 0.6 이상이면 강한 상관 관계로 볼 수 있다.
2) 상관 관계의 계산 : 상관 관계를 산출하는 방법은 측정 도구로 사용된 척도에 따라서 결정된다. 즉 서열 척도상에서 측정된 값을 이용해서 상관 계수를 산출할 경우에는 스피어맨(Speraman)의 p계수를, 등간 척도 혹은 비율 척도로 얻은 값에 근거해서 상관 계수를 산출할 경우에는 피어슨(Pearson) 상관 계수를 활용한다.
[출처] [통계] Spearman 등위상관계수|작성자 JIN
'ER study' 카테고리의 다른 글
| [통계] 척도의 종류 (0) | 2013.06.23 |
|---|---|
| [통계] 비모수 검정 nonparametrically (0) | 2013.06.23 |
| [통계] Sensitivity, specificity, Odds ratio (0) | 2013.06.19 |
| [통계, 펌글] Randomized controlled trial from wikipedia (0) | 2013.06.18 |
| [통계, 펌글] 범주형 자료 분석 : 왜 오즈비(odds ratio) vs 상대 위험도(relative risk) 를 만들었을까? (1) | 2013.06.18 |

